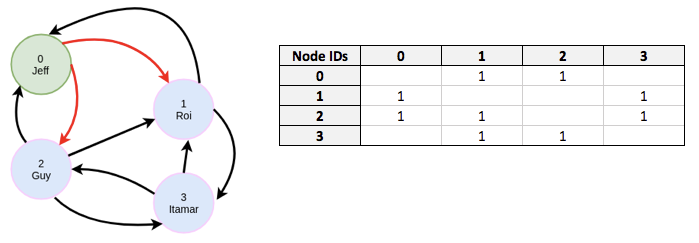
Fig 01 - A graph and corresponding adjacency matrix
Generally speaking, there are two ways to store and represent graphs. The first of these is the adjacency list, which consists of a list of all the nodes in the graph it represents, each paired with the set of nodes with which it shares an edge. This is effectively the industry standard. The second is the adjacency matrix, which represents its graph as a matrix with one row and column for each node within the graph. Within this matrix, nonzero values indicate the presence of an edge between the nodes represented by the corresponding row and column. An example of an adjacency matrix, alongside the graph it represents, is shown in Figure 1.
This method has several advantages in terms of performance. For example, determining whether two nodes share an edge is significantly faster when using matrix representation. Queries can be performed using direct mathematical operations such as matrix multiplication, which is often much faster than the traditional approach using adjacency lists. Performing a self-join, for instance, is simply a matter of multiplying a matrix by itself. Similarly, ingestion rates can be improved using adjacency matrices.
The vast majority of matrices representing real world graphs are ‘sparse’ – meaning that almost every value is zero – and RedisGraph stores adjacency matrices in Compressed Sparse Row (or CSR) format, meaning that they are, effectively, only storing nonzero values. This almost always results in a very large saving in terms of memory. Notably, storing matrices in CSR format does not impact RedisGraph’s ability to use them in mathematical operations.
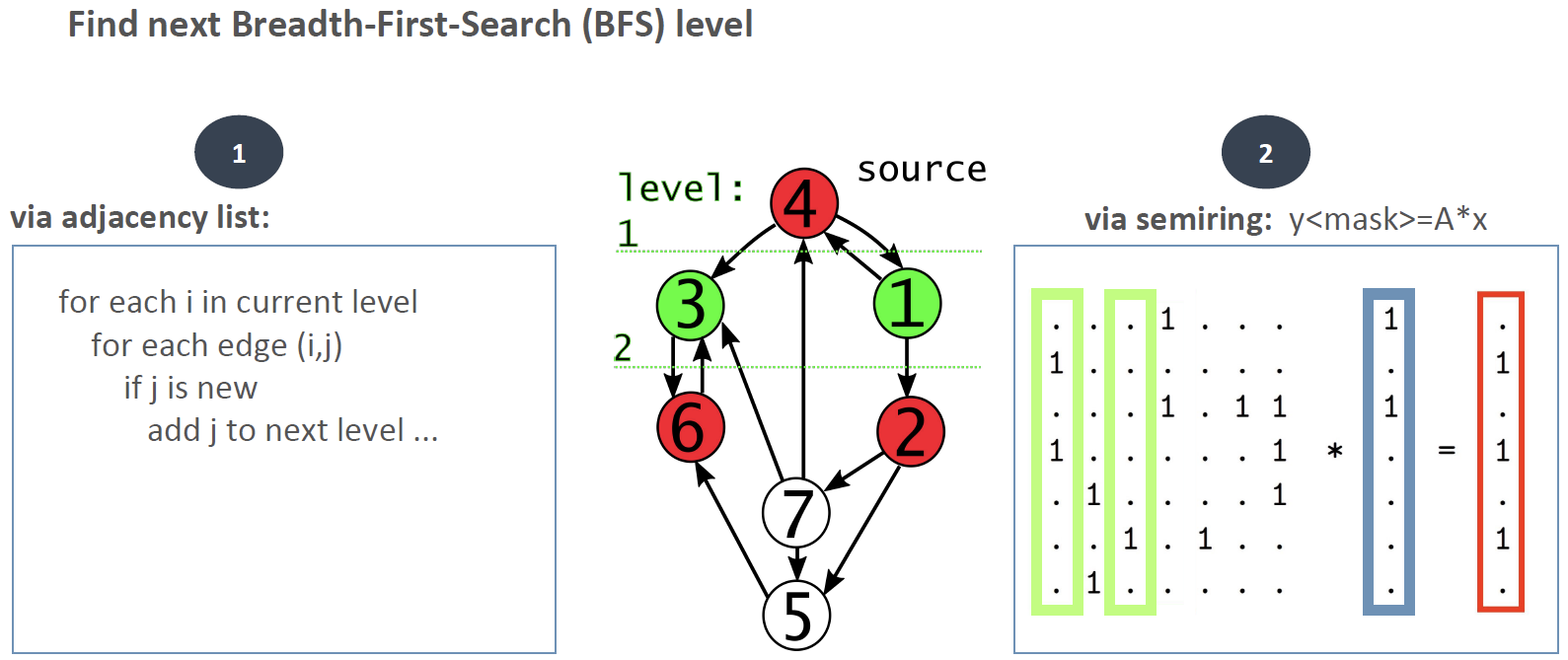
Fig 02 - Breadth-First-Search via adjacency lists and linear algebra
Going further, RedisGraph implements the GraphBLAS engine. GraphBLAS is an open effort whereby ‘BLAS’ stands for Basic Linear Algebra Subprograms. It provides the ability to use linear algebra running against sparse (compressed) matrices and this combination of optimises and simplifies many different graph queries and algorithms. For example, a comparison between implementations of Breadth-First- Search using linear algebra and the standard approach using adjacency lists is shown in Figure 2. It should be clear that the algebraic approach is easier to write and to understand. It is also computationally simpler.
There is one more advantage of the matrix representation that is worth noting. Matrix operations (such as multiplication) are extremely and easily parallelisable, and this property carries over to queries and graph algorithms based on linear algebra. This means that RedisGraph benefits very significantly from parallelisation. It will, in the future, be able to take full advantage of the massive parallelisation offered by GPU based processing.
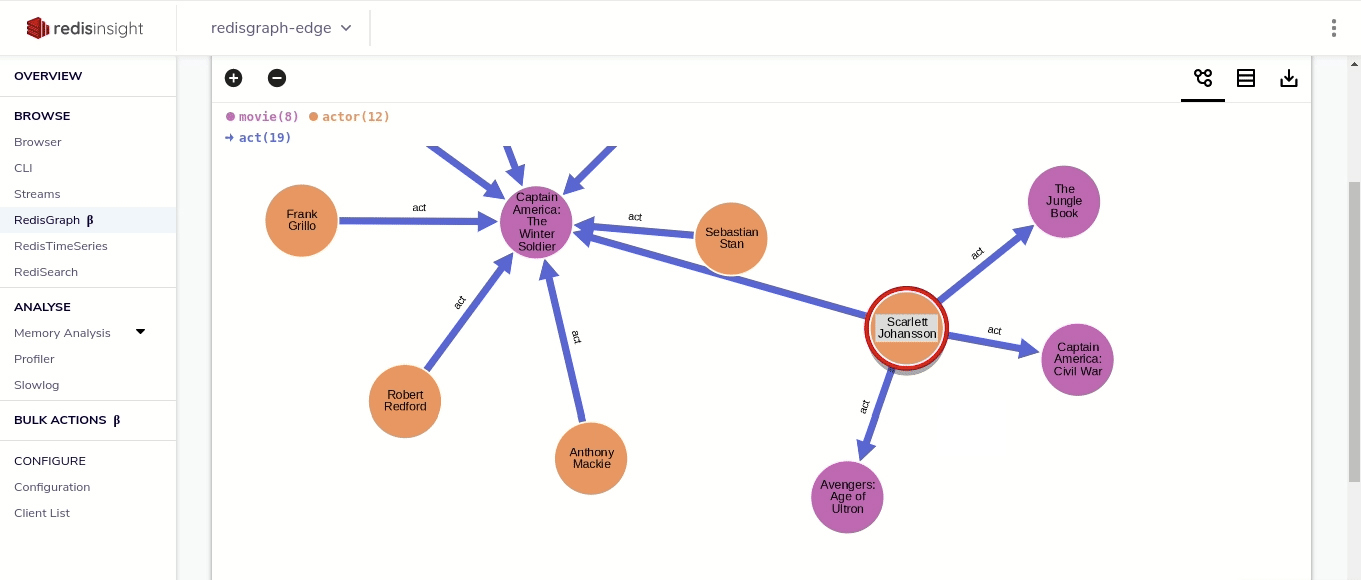
Fig 03 - Graph visualisation in RedisInsight
The 2.0 and 2.2 releases of RedisGraph offer a number of new features over previous versions. This includes various performance improvements, enhanced support for Cypher features, full-text search via RediSearch, and graph visualisation leveraging either RedisInsight (see Figure 3), Linkurious or Graphileon (Redis is partnered with the latter two). RedisGraph has also adopted the SuiteSparse implementation of GraphBLAS, which has positive implications for performance, as well LAGraph, an open source collection of GraphBLAS algorithms developed primarily for academia. A growing number of community created drivers and connectors are also available.